Un punto di vista è limitato di per sé.
Ci dà una visione a senso unico del paesaggio.
Solo quando si sommano più sguardi
complementari sulla stessa realtà si ha pieno
accesso al sapere delle cose. Quanto più è complesso
ciò che vogliamo comprendere, tanto più sarà
importante disporre di diverse paia d’occhi, in
modo che i fasci di luce convergano e possiamo
vedere l’Uno attraverso la molteplicità. È questa
la natura di una visione autentica: mettere
insieme i punti di vista già conosciuti e
mostrarne altri finora ignoti, insegnandoci che,
di fatto, sono tutti parte dello stesso Tutto.
Alexander Grothendieck
Spesso affermiamo che la scienza ufficiale sta arrivando a capire e a spiegare quello che gli antichi già da tempo sapevano attraverso l’intuizione o a qualche tipo di rivelazione. È vero, ma la scienza ha tempi e modalità diverse per affermare le stesse verità degli antichi. Il suo processo è molto più lento e laborioso. Un percorso fatto di duro lavoro di cesello e piccoli passi uno dietro l’altro, passi ben piantati a terra perché per guardare il Cosmo Urano (il cielo ordinato degli antichi) è necessario avere una solida base su cui appoggiarsi[1].
Un semplice esempio per comprenderci. Tutti “intuiamo” in qualche modo che 1 + 1 = 2. Ce lo dice l’aritmetica che studiamo a scuola da bambini, ma ce lo dice anche la nostra esperienza quotidiana, il nostro sapere empirico. Per la scienza, però, “intuire”, non è abbastanza, la scienza va avanti per “dimostrazioni formali” e la dimostrazione formale che 1 + 1 = 2 occupa le prime 300 pagine dei Principia Mathematica di Whitehead e Russell, un’opera monumentale il cui scopo (non riuscito) era quello di formalizzare le basi su cui si fonda tutta la matematica. Perché così tanto sforzo per dire che 1 + 1 = 2? Perché prima di tutto bisogna formalmente dichiarare quali sono gli attori in gioco. Cosa è “1”? Cosa è “2”? Cosa è “+”? E cosa è “=”? Può sembrare banale, ma quando Whitehead e Russell si posero queste domande, si aprì davanti a loro una voragine di una profondità inaspettata e per iniziare a dare una risposta a questi quesiti era necessario avere un linguaggio comune con il quale poter definire i concetti base. Questo linguaggio comune in cui tutta la matematica può essere espressa è la “Teoria degli Insiemi” di Cantor-Frege. Intorno alla metà del secolo scorso, Mac Lane ampliò questo linguaggio fondando la “Teoria delle Categorie”, che dava molta più espressività alla matematica e alle sue varie discipline come la geometria, l’algebra o la topologia. Negli anni ’60, Grothendieck ampliò ulteriormente questa teoria, generalizzandola e portandola all’essenza, introducendo il concetto di “Motivo” e di “Topos”. Ma all’inizio, per dimostrare che 1 + 1 = 2 e per rispondere alle domande per niente banali che ci siamo posti sopra, Whitehead e Russel usarono la teoria degli insiemi e quindi “1”, nei Principia Mathematica, è “L’Insieme di tutti gli Insiemi che contengono un solo elemento”. Allo stesso modo, “2” è “l’Insieme di tutti gli Insiemi che contengono due elementi”. “+” diventa un’operazione di unione logica tra insiemi e “=” è un concetto non banale di equivalenza che con Grothendieck e Morita raggiungerà la sua massima espressione di bellezza ed eleganza.

Alexander Grothendieck, che è stato definito l’Albert Einstein della matematica, ha usato lo strumento dell’astrazione per sondare le fondamenta della matematica sempre più a fondo fino ad arrivare al suo cuore. Per lui, qualsiasi dilemma si poteva semplificare se lo si guardava nella sua essenza. Non gli interessavano i numeri, le curve, le rette o qualsiasi altro oggetto matematico in particolare, ma la relazione tra essi. Aveva una sensibilità straordinaria nello scovare l’armonia fra le cose. Uno dei suoi maggiori colpi di genio fu quello di espandere la nozione di punto. Questo cessò di essere una posizione senza dimensioni e si animò di una complessa struttura interna che conteneva un universo infinito. Tutto ciò sfociò nel suddetto concetto di Topos. Guardare il mondo e la realtà con la lente dei Topoi è come astrarsi a tal punto che le parole del linguaggio naturale (che abbiamo inventato noi umani, mentre non è così per la matematica, come già Platone aveva intuito) non bastano a descrivere l’esperienza. È come osservare il “tutto” dalla prospettiva del “non tutto”, o il finito dalla ‘prospettiva’ del non-finito o Infinito, de-finito in queste pagine quale “velo dell’Assoluto”.
Questi sono luoghi del pensiero affascinanti e ricchi di incanto, ma anche estremamente pericolosi. Lo stesso Grothendieck scriveva: “anche in matematica certe cose dovrebbero rimanere segrete per sempre, per il bene di tutti noi”. Può sembrare esagerata un’affermazione di questo genere, ma come in fisica esistono dei mostri cosmici come i buchi neri che lacerano letteralmente lo spazio ed inghiottono qualsiasi cosa anche il tempo, in matematica esistono demoni che sono in grado di inghiottire e annientare persino il pensiero. Mostri che possono far impazzire studiosi di genio, come è successo a Gödel (di cui parleremo fra un po’) o a Grothendieck stesso, che scriveva: “l’umanità vive all’ombra di un nuovo orrore”, quello del “sonno della ragione” (F. Goya). Eppure, oltre i limiti della mente definita concreta dagli Insegnamenti esoterici, altre vibrazioni attendono di essere recepite dai livelli superiori dell’intelligenza sapiente.

E a proposito di “essenza” dobbiamo stare attenti a quale livello cercare il cuore dei fenomeni che vogliamo analizzare. Un esempio: diciamo spesso che Suono e Luce hanno la stessa essenza. Ma come fenomeni fisici, l’unica cosa che il suono e la luce hanno in comune è che sono due fenomeni vibrazionali. Basta, le analogie finiscono qui.
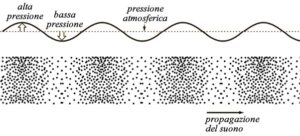
Il suono è la vibrazione molecolare di un mezzo fisico, che sia esso gassoso, liquido o solido; infatti, nello spazio vuoto (ovvero, per l’Antica Saggezza, semplicemente più sottile, presentando invece lo Spazio quale vivo o pieno di Vita), al di fuori dell’atmosfera terrestre, regna il silenzio più profondo e inudibile da mezzi fisici ordinari.
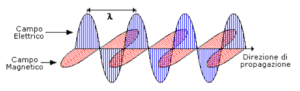
La luce è la vibrazione di un qualcosa completamente diverso rispetto al suono, è la vibrazione di un campo: il campo elettromagnetico che può propagarsi anche nel ‘vuoto’ dello spazio profondo; e l’Universo stesso ha una vibrazione di natura ancora diversa da suono e luce, la sua è la vibrazione di un altro campo: il Campo di Higgs, responsabile di tutto ciò che è in manifestazione, compreso l’Universo stesso che a sua volta è una caratteristica manifesta del campo gravitazionale. Questo per dire che affermare che suono e luce hanno la stessa essenza presuppone una conoscenza condivisa del significato della parola Essenza, che non è quello della loro manifestazione fisica, ove le due entità non sono intercambiabili. Nella Filosofia occulta con le Idee di Suono e Luce non si intendono quindi le loro controparti fenomeniche o fisiche, bensì la Vibrazione della Vita ai vari livelli della Sostanza spaziale.

Come Grothendieck, anche Kurt Gödel era interessato all’essenza intesa come verità astratta o cuore della matematica e per ricercare questa essenza ha rivolto il potere del formalismo matematico verso la matematica stessa[2]. Quello che ha scoperto ha segnato per sempre il mondo della logica e della matematica, individuando nella sua ‘essenza’ la medesima natura di “indeterminazione”[3] che Heisenberg aveva riscontrato nei fondamenti della Fisica qualche anno prima. Detto in maniera semplice, quello che Gödel ha scoperto è che in sistemi matematici formali, come ad esempio l’aritmetica, esistono delle affermazioni sui numeri che sono vere, ma la cui verità non può essere dimostrata usando l’aritmetica stessa. Quindi qualsiasi sistema formale, ad esempio un qualsiasi sistema numerico, è per sua natura incompleto (ecco perché è fallito il progetto di Whitehead e Russell). Presuppone l’intervento di un piano di osservazione o comprensione diverso da quello del raziocinio intellettuale dell’indagine matematica.
Matematica, maqhmatikóV, come termine, si riferisce a tutto quello che è relativo allo studio, all’apprendimento e alla conoscenza, ma Grothendieck, Gödel e Heisenberg hanno segnato dei limiti oltre i quali non ci è dato andare in questa conoscenza intellettiva. Ci sono “orizzonti degli eventi” oltre i quali tutto, spazio, tempo, pensiero, perdono di significato. Questi grandi pensatori ci hanno detto che per quanto il nostro studio sia profondo e appassionato, esisteranno sempre delle verità che ci sono precluse in questa manifestazione e questo la scienza lo ha imparato già dagli anni ’30 del secolo scorso. Per quanti sforzi l’umanità possa fare esistono barriere, veli, oltre i quali il nostro sguardo fisico non può andare. Dobbiamo accettarlo e questo è valido per ogni tipo di “insegnamento” appreso solo attraverso certi livelli della mente. Ovvero, questo non vuol dire che la scienza sia limitata rispetto all’intuizione o alla possibilità di sviluppare gli strumenti di percezione di tutto ciò che “ci risuona in qualche modo”. I limiti conoscitivi sono universali o proporzionali ai vari livelli di ‘realtà’ o coscienza e gli insegnamenti sapienziali affermano che: “l’Umanità potrà accedere ad alcuni livelli di comprensione solo quando sarà pronta”.
Il linguaggio che la scienza usa per descrivere questi limiti è molto complicato, per pochi “discepoli”, come complicato è il linguaggio dell’esoterismo che è riservato a chi è dedito al suo studio. Noi tutti, scienziati ed esoteristi, dobbiamo sforzarci perché questi linguaggi convergano sempre di più e perché gli scienziati non vedano come ciarlatani gli esoteristi e gli esoteristi non considerino ciechi e sordi gli scienziati. Come Grothendieck scriveva nella citazione all’inizio di questo articolo, solo con uno sguardo comune si potrà riconoscere che si è parte di uno stesso Tutto.
È importante che, per ogni disciplina di studio e ricerca, si proceda con mente aperta e curiosità, così da arrivare a costruire ponti di pensiero, collegamenti e quindi linguaggi comuni che rispettino le categorie di senso di ogni “scienza” portando a quell’unificazione della conoscenza e dello studio che, nei secoli, abbiamo scordato.
[1] Quello che si definisce “Metodo Scientifico” si basa sull’osservazione del fenomeno, sulla teorizzazione di questo fenomeno e sulla sperimentazione per verificare la teoria ipotizzata.
[2] Questo viene definito un procedimento “metamatematico”.
[3] Impossibile qui spiegare in maniera esaustiva la formidabile scoperta di Gödel che sono i “teoremi di Incompletezza Sintattica”. In linguaggio comune potremmo riassumere il suo risultato dicendo che qualunque sistema formale S in cui può essere sviluppato un certo ammontare di aritmetica e che soddisfa alcune condizioni minimali di coerenza (non ci sono contraddizioni) è incompleto: si può costruire un enunciato aritmetico elementare A tale che né A né la sua negazione sono dimostrabili in S. In effetti, l’enunciato così costruito è allora vero (nel senso che è possibile) dal momento che esso esprime la propria indimostrabilità in S, attraverso una rappresentazione nell’aritmetica della sintassi di S. Inoltre, si può costruire nell’aritmetica un enunciato C che esprime la coerenza di S, e C non è dimostrabile in S se S è coerente.





