Glossario – Numero
Etimo secondo TPS
Dal latino numerus, dalla radice indoeuropea *NEM-, che esprime l’idea di distribuire equamente. Ha lo stesso etimo il latino nemus, bosco sacro dove si amministrava la giustizia. Greco nemo, distribuisco con giustizia, amministro, regolo; nomos, legge; nemesis, giustizia divina.
Il numero è l’Entità che governa la distribuzione energetica
Treccani
nùmero s. m. [dal lat. numĕrus; cfr. novero]. –
1. Ciascuno degli enti astratti che rappresentano insiemi di unità, ordinati in una successione infinita (serie naturale dei n.) nella quale ogni elemento conta un’unità in più rispetto al precedente; tali enti, fatti corrispondere ciascuno a ciascuno degli oggetti che costituiscono un insieme, servono a contarli (numerarli), e quindi a indicarne la quantità (anch’essa detta numero): il n. dei libri, dei voti, delle automobili in circolazione, degli alunni di una scuola; il loro n. è di novanta; sono in n. di (arrivano al n. di, superano il n. di) trecento; oppure a indicare il posto occupato da un singolo oggetto in una serie (n. d’ordine): la sua sedia è il n. 15 della terza fila. In usi assol., seguito dal nome del numero, quando si consideri il numero in sé, come ente astratto, non riferito a oggetti: il n. 5, il n. 11, il n. 999, ecc.; si ritiene che il n. 13 porti fortuna (spesso numero è sottinteso: il 13 porta fortuna; il 3 è un n. perfetto). In matematica, più precisamente, n. naturali, i numeri nei significati sopra definiti, ulteriormente qualificati come n. cardinali (insiemi di unità), e n. ordinali (posti occupati in una successione); n. interi (o n. relativi), costituenti un’estensione dei numeri naturali, in quanto comprendono, oltre questi, lo zero e i n. negativi (minori di zero): tale insieme, nel quale è sempre possibile la sottrazione, è adatto per la rappresentazione di quantità discrete variabili in due versi opposti; n. pari, i numeri interi divisibili per due; n. dispari, i numeri interi non divisibili per due; n. primi, i numeri naturali che non possono essere ottenuti moltiplicando due altri numeri naturali, come per es. 2, 3, 5, 7, 11, ecc.; n. primi tra loro, due numeri naturali che non hanno alcun divisore comune eccettuato il numero 1; n. perfetti, quei numeri naturali che sono uguali alla somma dei loro divisori (eccettuato il numero stesso): per es., 6 (= 1 + 2 + 3), che è il più piccolo; n. frazionarî, i numeri che si esprimono con una frazione, cioè con un rapporto tra due numeri interi, come per es. 2/3, 5/7, ecc.; n. decimali, i numeri costituiti da una parte intera e da una parte decimale (nella quale si hanno, nell’ordine, le cifre dei decimi, dei centesimi, dei millesimi, ecc.), separate da una virgola o, secondo l’usanza anglosassone, da un punto: ogni numero decimale con un numero di cifre finito oppure periodico (nel quale cioè un gruppo di cifre si ripete indefinitamente) è riconducibile a una frazione; n. razionali, che comprendono i numeri interi e i numeri frazionarî, e costituiscono un insieme nel quale è sempre possibile la divisione (tranne che per lo zero); n. irrazionali, i numeri dati dal rapporto tra due grandezze omogenee non commensurabili tra loro (per es., il lato di un quadrato e la sua diagonale), tali cioè che la misura di una di esse, prendendo come unità di misura l’altra, non possa essere espressa da un numero razionale: per es., Ω, Ψ, e (numero di Nepero, base dei logaritmi naturali), π (rapporto tra una circonferenza e il suo diametro), ecc.; n. reali, l’insieme dei numeri razionali e dei numeri irrazionali, che può essere posto in corrispondenza biunivoca con tutti i punti di una retta ed è quindi alla base del calcolo delle grandezze variabili con continuità, ossia dell’analisi matematica; n. immaginarî, i numeri dati dal prodotto di un numero reale e del numero i, detto unità immaginaria, tale che i2 = − 1; n. complessi, i numeri che si rappresentano come somma di un numero reale e di un numero immaginario, e che contengono in sé come caso particolare i numeri reali, ai quali si riducono qualora il coefficiente dell’unità immaginaria sia nullo: rendono possibile l’estrazione di radice da un numero negativo, e quindi la soluzione di ogni equazione algebrica a coefficienti reali (o anche complessi); n. algebrici, i numeri, reali o complessi, che sono soluzione di un’equazione algebrica a coefficienti razionali; n. trascendenti, i numeri non algebrici, come per es. il numero e, il numero π, ecc. Per i n. transfiniti e per altre specie di numeri, v. ai singoli aggettivi. Teoria dei n., lo studio delle proprietà dei numeri naturali, come la scomponibilità in fattori primi, la ricerca delle soluzioni intere di equazioni, o di sistemi di equazioni, lineari o algebriche a coefficienti interi: si distinguono una teoria elementare dei n., e una teoria analitica dei n., che si avvale della teoria delle funzioni di variabile reale o complessa e di altre parti dell’analisi. Nel calcolo delle probabilità, legge dei grandi n., teorema per il quale, in un grande numero di prove, la frequenza relativa di un evento (cioè il rapporto tra il numero dei casi in cui l’evento si verifica e il numero delle prove) tende al valore numerico della probabilità dell’evento stesso, per cui all’aumentare del numero delle prove lo scarto tra la frequenza e la probabilità tende a zero: per es., considerando una successione indefinita di lanci di un dado, ciascun numero tenderà a uscire con una frequenza relativa di una volta ogni sei, pari alla probabilità, che è appunto di 1/6.
Leggi la definizione direttamente sul dizionario.
Wikipedia
In matematica, un numero è un modo di esprimere sia una quantità, sia la posizione in un elenco di elementi, sia il rapporto tra grandezze dello stesso tipo.[1] Storicamente il concetto di numero nasce, con la storia dell’uomo, per motivi pratici legati alla necessità del conteggio, quindi come astrazione simbolica del concetto di quantità, inizialmente realizzato attraverso una corrispondenza biunivoca tra elementi di due insiemi diversi.
Si definisce operazione numerica una procedura che, a partire da uno o più numeri, genera un altro numero. Le operazioni numeriche fondamentali (dette anche “operazioni aritmetiche”) sono: l’addizione, la sottrazione, la moltiplicazione e la divisione. Lo studio delle proprietà di queste operazioni è parte dell’algebra elementare.
Un numero che esprime la dimensione di un insieme di elementi, così come un numero che identifica la posizione in una successione di oggetti, è detto numero naturale. La necessità di esprimere una grandezza in relazione ad un’altra grandezza ha reso necessaria l’introduzione di classi più ampie di numeri, come i numeri razionali ed i numeri reali. L’esigenza di rappresentare il numero ottenuto attraverso un’operazione matematica, infine, ha giustificato l’utilizzo di ulteriori classi di numeri come, ad esempio, i numeri algebrici.
Numeri naturali
Durante la storia della matematica sono stati definiti diversi insiemi numerici, tra cui i numeri naturali, che sono:
1, 2, 3, 4 …
I numeri naturali (il cui insieme è indicato con il simbolo ![]() ) sono usati per contare. La presenza dello zero fra i numeri naturali dipende dalla convenzione scelta. Lo zero è comunque previsto dagli assiomi di Peano.
) sono usati per contare. La presenza dello zero fra i numeri naturali dipende dalla convenzione scelta. Lo zero è comunque previsto dagli assiomi di Peano.
L’insieme dei numeri naturali costituisce una successione ordinata, ed ogni numero è generalmente descritto tramite una o più cifre.
Numeri interi relativi
Se a partire dall’insieme dei numeri naturali si introduce la differenza di segno (e lo zero se non già incluso tra i numeri naturali), distinguendo tra numeri positivi e numeri negativi, si ottengono i numeri interi relativi (o semplicemente interi), il cui insieme è indicato con il simbolo ![]() . I numeri interi sono:
. I numeri interi sono:
… -3, -2, -1, 0, 1, 2, …
Numeri razionali
Se a partire dai numeri interi si costruiscono i numeri dati dal loro rapporto, si ottengono i numeri razionali, i quali sono quindi esprimibili tramite una frazione (ratio in latino, da cui il nome di numeri “razionali”). Ad esempio:
![]()
L’insieme di tutti i numeri razionali è solitamente indicato col simbolo ![]() .
.
Numeri algebrici
I numeri algebrici sono tutti i numeri ottenibili come radici di equazioni algebriche a coefficienti interi. I numeri razionali sono tutti algebrici, ma molti numeri algebrici non sono razionali. Ad esempio:
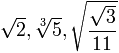
sono numeri algebrici che non possono essere descritti tramite una frazione.
Un numero non algebrico è detto trascendente. Ad esempio, ![]() (pi greco) ed
(pi greco) ed ![]() sono trascendenti: non è possibile ottenere
sono trascendenti: non è possibile ottenere ![]() come radice di un polinomio a coefficienti interi.
come radice di un polinomio a coefficienti interi.
Numeri reali
L’insieme dei numeri reali comprende tutti i numeri esprimibili, con o senza la virgola, tramite il sistema numerico decimale. I numeri reali comprendono tutti i numeri elencati precedentemente. In particolare i numeri reali si dividono in razionali e irrazionali, oppure in algebrici e trascendenti.
L’insieme dei numeri reali è simboleggiato con ![]() .
.
Numeri computabili
Sono i numeri reali esprimibili con una notazione posizionale in una qualche base e sono costituiti da una sequenza finita di cifre o da una successione illimitata di cifre che può essere generata da una procedura ben definita in grado di operare illimitatamente.
Numeri complessi
L’insieme dei numeri reali non è sufficiente a fornire tutte le soluzioni delle equazioni algebriche. Per esempio, l’equazione:
![]()
non ha soluzioni nel campo dei numeri reali, perché in questo insieme il quadrato di un numero è sempre positivo. Per risolvere questo problema, è stata introdotta l’unità immaginaria, tale che:
![]()
Tale numero non appartiene all’insieme dei numeri reali, bensì all’insieme dei numeri complessi. Più in generale, un numero complesso è una espressione del tipo:
![]()
dove è ![]() l’unità immaginaria e
l’unità immaginaria e ![]() sono numeri reali. L’insieme dei numeri complessi è indicato con il simbolo
sono numeri reali. L’insieme dei numeri complessi è indicato con il simbolo ![]() .
.
Gli insiemi numerici seguenti sono ciascuno sottoinsieme dell’altro, secondo quest’ordine (dove il simbolo ![]() indica l’inclusione stretta):
indica l’inclusione stretta):
![]()
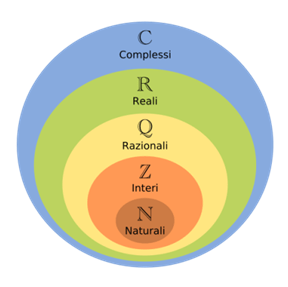
Diagramma di Venn di alcuni insiemi numerici notevoli
Leggi la definizione direttamente su Wikipedia.






Pingback:Sesto aspetto dell’Ordine - TPS Blog - Area italiana