Glossario – Matematica
Etimo secondo TPS
Dal termine latino mathematĭca (sottintesa ars), mutuato dal greco mathematiké (sottintesa techne, arte). Si sviluppa dalla radice indoeuropea *MA-, che esprime l’idea della misura, intesa sia come limite sia come rapporto: in sanscrito mā significa “misurare”, e lo stesso senso ha il greco metréo e il latino metior.
La radice si sviluppa nelle forme mad/med/mel per esprimere in concetto di “avere cura di”, “medicare”: si veda il latino medicus, medico, meditor, riflettere; il greco medéo, prendersi cura di; melodèo, cantare, suonare una melodia; melodía, canto. Mad/med si trasforma spesso in mat/met, e deriva appunto da questa variante anche la parola considerata (DEC, pp. 283, 294-295).
Matematica indica la misura dei rapporti spaziali
Nel Lambdoma Ordine la definizione è: La Matematica è la scienza divina del Numero (5.1)
Treccani
matemàtica (ant. e raro mattemàtica) s. f. [dal lat. mathematĭca (sottint. ars), gr. μαϑηματική (sottint. τέχνη); v. matematico]. –
1.a. Originariamente, la scienza razionale dei numeri (aritmetica, intesa come scienza della quantità discreta) e delle misure (geometria, intesa come scienza dell’estensione, cioè della quantità continua), i cui primi sviluppi, presso le civiltà preelleniche (Babilonia, Egitto), sono in relazione con la ricerca di soluzioni a concreti problemi di calcolo (computo commerciale, agrimensura, navigazione, ecc.). Nella Grecia antica, tale scienza si configura come rigoroso sistema deduttivo (spec. nella sintesi euclidea della geometria) e come forma di conoscenza, per Platone intermedia tra la conoscenza sensibile e la scienza contemplativa delle idee, per Aristotele capace di astrarre dal dato sensibile per raggiungere conclusioni vere e certe anche sul sensibile stesso (alla diffusione della tradizione aristotelica può essere ricondotta l’espressione proverbiale la m. non è un’opinione). A partire dal Cinquecento, anche grazie all’adozione del sistema di notazione numerica posizionale (inventato dagli Indiani e adottato dagli Arabi), si sviluppa nell’occidente la nuova branca dell’algebra, sulla base delle convenzioni e delle regole per il calcolo già individuate dagli Arabi; successivamente, la matematica passa a comprendere la geometria analitica, che applica i metodi dell’algebra alla soluzione di problemi geometrici, e il calcolo infinitesimale, che, mentre tende a svincolare il concetto di continuità dalle rappresentazioni geometriche, pone le basi per lo studio delle funzioni, nonché per la spiegazione matematica del moto dei corpi (meccanica razionale): tali progressi sono generalm. interpretati (Galilei, Cartesio, Kant) come frutto di un’intuizione assoluta della verità, che solo la matematica può produrre in quanto conoscenza certa, evidente, necessaria di enti oggettivi e immutabili.
1.b. Nell’Ottocento e nel Novecento, il suddividersi della ricerca matematica in numerosi indirizzi, alcuni dei quali ampiamente autonomi, ha reso ardua la formulazione di una definizione univoca della matematica come scienza, pur potendosi individuare alcuni caratteri comuni, quali un progressivo abbandono dei criterî di evidenza intuitiva, un crescente grado di generalizzazione, astrazione e formalizzazione, e l’adozione generalizzata del metodo assiomatico-deduttivo. Tali tendenze risultano evidenti in alcune fondamentali linee di sviluppo: l’analisi matematica, nata dal calcolo infinitesimale, si occupa delle funzioni e delle operazioni su di esse prescindendo da ogni riferimento all’intuizione geometrica e fisica; l’algebra, generalizzando il proprio campo di applicazione (geometria algebrica, teoria dei gruppi, algebra delle matrici, calcolo vettoriale), finirà per costituirsi nel 20° secolo (come algebra astratta) in teoria generale delle proprietà formali delle operazioni (non più solo numeriche); nell’ambito della geometria si costituiscono geometrie non euclidee (col conseguente abbandono della concezione intuitiva dello spazio) e, successivamente, si sviluppa la topologia, che assume come oggetto proprietà «qualitative» (cosicché la quantità non può più essere considerata l’oggetto esclusivo della matematica); in base alla teoria degli insiemi, i numeri (interi, reali, ecc.) possono essere visti come oggetti, dotati di certe proprietà, che formano particolari insiemi, i quali possono ora essere studiati nelle loro implicazioni logico-formali (problema dei fondamenti della m.), secondo un orientamento (logicismo) che si propone l’identificazione dell’edificio formale della matematica con un sistema logico (logica matematica) nella cui coerenza interna trovino giustificazione gli enti e gli asserti matematici, mentre alla ridefinizione della matematica come scienza che ha per oggetto la manipolazione secondo determinate regole di simboli di per sé privi di significato (formalismo) si oppone, ritenendola responsabile di conseguenze paradossali (v. paradosso1), una concezione per la quale sono oggetto della matematica soltanto costruzioni mentali dotate di caratteristiche di evidenza e intuitività (intuizionismo).
1.c. Nella matematica contemporanea, il progresso delle tecniche di calcolo elettronico consente lo sviluppo di indirizzi della ricerca matematica che affrontano problemi non risolvibili se non con l’applicazione di algoritmi estremamente complessi; d’altra parte, l’elaborazione di teorie matematiche capaci di spiegare fenomeni in larga parte dovuti al caso ha portato alla considerazione di concetti statistico-probabilistici che, grazie a tali nuove tecniche di calcolo, hanno esteso il campo d’indagine della matematica al di là di ciò che è certo in senso deterministico; nel permanere di una pluralità di settori (per cui al sing. matematica si preferisce talvolta il plur. le matematiche), le tradizionali classificazioni in branche (quali la geometria, l’analisi, l’algebra, ecc.) vanno progressivamente perdendo d’importanza, mentre emergono connessioni che individuano substrati comuni, per lo più identificabili in strutture algebriche e topologiche: in tal senso la matematica potrebbe definirsi come la scienza delle strutture e delle relazioni astratte.
2. Tradizionalmente si distinguono una m. pura, che studia i problemi matematici indipendentemente da una loro possibile utilizzazione pratica, e una m. applicata, cui compete l’elaborazione di strumenti e modelli adatti agli scopi di altre scienze (fisica, chimica, biologia, ecc.) e della tecnica. In relazione all’insegnamento della matematica nelle scuole: cattedra di m. e fisica nei licei; un’ora, una lezione di m.; insegnare, studiare m.; un testo di m. per le scuole medie.
Leggi la definizione direttamente sul dizionario
Wikipedia

Euclide, matematico greco, immaginato da Raffaello nella sua opera Scuola di Atene
La matematica (dal greco μάθημα (máthema), traducibile con i termini “scienza”, “conoscenza” o “apprendimento”; μαθηματικός (mathematikós) significa “incline ad apprendere”) è la disciplina che studia le quantità, i numeri, lo spazio, le strutture e i calcoli.
Col termine matematica di solito si designa la disciplina (e il relativo corpo di conoscenze) che studia problemi concernenti quantità, estensioni e figure spaziali, movimenti di corpi, e tutte le strutture che permettono di trattare questi aspetti in modo generale. La matematica fa largo uso degli strumenti della logica e sviluppa le proprie conoscenze nel quadro di sistemi ipotetico-deduttivi che, a partire da definizioni rigorose e da assiomi riguardanti proprietà degli oggetti definiti (risultati da un procedimento di astrazione, come triangoli, funzioni, vettori ecc.), raggiunge nuove certezze, per mezzo delle dimostrazioni, attorno a proprietà meno intuitive degli oggetti stessi (espresse dai teoremi).
La potenza e la generalità dei risultati della matematica le ha reso l’appellativo di regina delle scienze: ogni disciplina scientifica o tecnica, dalla fisica all’ingegneria, dall’economia all’informatica, fa largo uso degli strumenti di analisi, di calcolo e di modellazione offerti dalla matematica.
Descrizione
Evoluzione e finalità della matematica

Papiro egiziano che tratta di matematica
La matematica ha una lunga tradizione presso tutti i popoli della storia antica e moderna; è stata la prima disciplina a dotarsi di metodi di elevato rigore e portata. Ha progressivamente ampliato gli argomenti della sua indagine e progressivamente ha esteso i settori ai quali può fornire aiuti computazionali e di modellazione. È significativo che, in talune lingue e in talune situazioni, al termine singolare si preferisca il plurale matematiche.
Nel corso della sua lunga storia e nei diversi ambienti culturali si sono avuti periodi di grandi progressi e periodi di stagnazione degli studi. Questo in parte è dovuto a singoli personaggi, capaci di dare apporti profondamente innovativi e illuminanti e di stimolare all’indagine matematica grazie alle loro doti didattiche. Si sono avuti anche periodi di arretramento delle conoscenze e dei metodi, specie in relazione a eventi distruttivi o a periodi di decadenza complessiva della vita intellettuale e civile. Negli ultimi 500 anni, per il miglioramento dei mezzi di comunicazione, è prevalsa la crescita del patrimonio di risultati e di metodi, dovuta alla natura stessa delle attività matematiche, tese alla esposizione precisa di problemi e soluzioni; ciò impone di comunicare col fine ultimo di chiarire ogni dettaglio delle costruzioni logiche e dei risultati (alcuni chiarimenti richiedono un impegno non trascurabile, talora molti decenni). Questo ha corrisposto alla definizione di un linguaggio, strumento esemplare per la trasmissione e la sistemazione delle conoscenze.
Non va dimenticato che nell’antichità (più precisamente nel periodo ellenistico), con “matematica” ci si riferisce ad un insieme di discipline (geometria, meccanica, ottica, idrostatica, astronomia, geografia matematica, teoria musicale e altre), ossia essa configurava nell’insieme una scienza – si veda al senso etimologico del termine – con rigorosa struttura logica interna e saldi rapporti con applicazioni, ossia avente connessioni con la tecnologia. La scienza antica si è estinta in alcune “ondate distruttive”, progressivamente è rinata suddivisa in varie discipline più circoscritte.
Il linguaggio e il rigore matematico

Eulero, che ha creato e reso popolare gran parte della notazione matematica correntemente utilizzata
Del linguaggio matematico moderno, fatto di simboli riconosciuti in tutto il mondo, la maggior parte è stata introdotta dopo il XVI secolo. Prima di allora la matematica era scritta usando parole, un processo faticoso che rallentava le scoperte matematiche. Eulero (1707-1783) è stato il responsabile di molte delle notazioni oggi in uso. La notazione matematica moderna rende molto più facile il lavoro del matematico, ma i principianti lo trovano scoraggiante. È estremamente compressa: pochi simboli contengono una grande quantità di informazioni; come le note musicali, la notazione matematica moderna ha una sintassi rigorosa (che in misura limitata varia da autore ad autore, e da disciplina a disciplina) e codifica informazioni difficili da scrivere in qualsiasi altro modo.
Il simbolo dell’infinito (∞) in caratteri tipografici diversi
Il linguaggio matematico può essere difficile per i principianti. Parole come o e solo hanno precisi significati, più che nella lingua corrente. Inoltre, parole come aperto e campo hanno specifici significati matematici. Il gergo matematico comprende moltissimi termini tecnici, come omeomorfismo e integrabile, perché la matematica richiede assai più precisione del linguaggio quotidiano.
Nelle dimostrazioni matematiche è fondamentale il rigore. Per rigore si intende un utilizzo preciso e logico di teoremi già dimostrati, in modo che, analizzando la dimostrazione in profondità attraverso un processo a ritroso, si arrivi ad assiomi e definizioni universalmente accettati. Il livello di rigore richiesto in matematica è variato col tempo: i Greci richiedevano argomentazioni dettagliate, ma nel periodo di Isaac Newton il rigore utilizzato nelle dimostrazioni si era alleggerito. I problemi nati dalle definizioni usate da Newton hanno portato alla rinascita di una attenta analisi delle dimostrazioni nel corso del Diciannovesimo secolo. Il significato di rigore matematico non è sempre chiaro. Ad esempio i matematici continuano a discutere sull’opportunità di considerare valide le dimostrazioni effettuate attraverso computer: dato che lunghi calcoli sono difficili da verificare, tali dimostrazioni potrebbero essere considerate non sufficientemente rigorose.
Gli assiomi, nel pensiero tradizionale, erano considerati le “verità auto-evidenti”, ma questa concezione comporta alcuni problemi. A livello formale, un assioma è solo una successione di simboli, che ha un significato intrinseco solo nel contesto di tutte le formule derivabili di un sistema assiomatico. L’obiettivo del programma di Hilbert è stato proprio quello di fornire l’intera matematica di una solida base assiomatica, ma secondo il teorema di incompletezza di Gödel una completa assiomatizzazione della matematica è impossibile. Nonostante ciò, la matematica è spesso immaginata consistere (per lo meno nel suo contenuto formale) nella teoria degli insiemi in una qualche assiomatizzazione, nel senso che ogni enunciato matematico, o dimostrazione, può essere scritto con formule esprimibili all’interno di tale teoria.
Matematica teorica e applicata
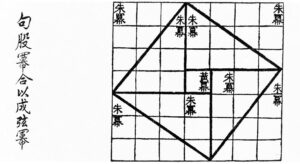
Teorema di Pitagora in uno scritto cinese datato tra il 500 a.C. e il 200 a.C.. Il teorema ha importanti ricadute pratiche e teoriche
Le attività matematiche sono naturalmente interessate alle possibili generalizzazioni e astrazioni, in relazione alle economie di pensiero e ai miglioramenti degli strumenti (in particolare degli strumenti di calcolo) che esse sono portate a realizzare. Le generalizzazioni e le astrazioni quindi spesso conducono a visioni più approfondite dei problemi e stabiliscono rilevanti sinergie tra progetti di indagine inizialmente rivolti a obiettivi non collegati.
Nel corso dello sviluppo della matematica si possono rilevare periodi e ambienti nei quali prevalgono alternativamente atteggiamenti generali e valori riconducibili a due differenti generi di motivazioni e di approcci: le motivazioni applicative, con la loro spinta a individuare procedimenti efficaci, e le esigenze di sistemazione concettuale con la loro sollecitazione verso generalizzazioni, astrazioni e panoramiche strutturali.
Si tratta di due generi di atteggiamenti tra i quali si costituisce una certa polarizzazione; questa talora può diventare contrapposizione, anche astiosa, ma in molte circostanze i due atteggiamenti stabiliscono rapporti di reciproco arricchimento e sviluppano sinergie. Nel lungo sviluppo della matematica si sono avuti periodi di prevalenza di uno o dell’altro dei due atteggiamenti e dei rispettivi sistemi di valori.
Del resto la stessa nascita della matematica può ragionevolmente ricondursi a due ordini di interessi: da un lato le esigenze applicative che fanno ricercare valutazioni praticabili; dall’altro la ricerca di verità tutt’altro che evidenti, forse tenute nascoste, che risponde a esigenze immateriali, la cui natura può essere filosofica, religiosa o estetica.
Negli ultimi 30 o 40 anni tra i due atteggiamenti si riscontra un certo equilibrio non privo di tensioni riemergenti, ma con molteplici episodi di mutuo supporto. A questo stato di cose contribuisce non poco la crescita del mondo del computer, rispetto al quale il mondo della matematica presenta sia canali di collegamento (che è ormai assurdo cercare di interrompere) sia differenze, ad esempio differenze dovute a diverse velocità di mutazione e a diversi stili comunicativi, che proiettano le due discipline agli antipodi.
Argomenti principali

Tavola aritmetica per bambini, Losanna 1835
Cerchiamo ora di segnalare a grandi linee i temi dell’indagine matematica, illustrando una sorta di itinerario per un progressivo accostamento dei problemi, delle argomentazioni e delle sistemazioni teoriche.
Aritmetica
I primi problemi che inducono ad accostarsi alla matematica sono quelli che si possono affrontare con l’aritmetica elementare: i calcoli eseguibili con le quattro operazioni possono riguardare contabilità finanziarie, valutazioni di grandezze geometriche o meccaniche, calcoli relativi agli oggetti e alle tecniche che si incontrano nella vita quotidiana.
I più semplici di questi calcoli possono effettuarsi servendosi solo di numeri interi naturali, ma presto i problemi di calcolo richiedono di saper trattare i numeri interi relativi e i numeri razionali.
Algebra

Pagina di Algebra di al-Khwarizmi
I problemi aritmetici più semplici sono risolti mediante formule che forniscono risultati conseguenti. Ad esempio: l’area di un rettangolo con lati lunghi 3 e 5 è il loro prodotto 3 \times 5 = 15 . Complicando gli enunciati diventa necessario servirsi di equazioni. Ad esempio: per il teorema di Pitagora, se un triangolo rettangolo ha i lati più corti (cateti) di lunghezza 3 e 4 , quello più lungo (ipotenusa) ha come lunghezza il numero positivo x che risolve l’equazione:
x2 – 32 – 42 = 0.
Le equazioni più semplici sono le equazioni lineari, sia perché rappresentano le questioni geometriche più semplici, sia perché sono risolvibili con procedimenti standard.
Nelle formule e nelle equazioni conviene far entrare parametri con valori indeterminati: in tal modo si viene a disporre di strumenti di portata più generale, che permettono di conseguire evidenti economie di pensiero. Ad esempio: in un triangolo rettangolo con cateti di lunghezza a e b, la lunghezza dell’ipotenusa è il numero positivo x tale che x2 -a2 – b2 = 0. Per meglio valutare le formule e per risolvere molti tipi di equazioni è necessario sviluppare un calcolo letterale che permetta di rimaneggiarle. Le regole di questo calcolo letterale costituiscono la cosiddetta algebra elementare.
L’algebra moderna si occupa anche dello studio delle relazioni fra insiemi e delle strutture algebriche, cioè strutture che caratterizzano insiemi concreti (come i numeri) o astratti sui quali è stata definita una o più operazioni.
Geometria
Lo studio della geometria piana e spaziale riguarda inizialmente concetti primitivi: il punto, la retta, il piano. Combinando questi elementi nel piano o nello spazio si ottengono altri oggetti quali segmenti, angoli, angoli solidi, poligoni e poliedri.
Punto, retta, piano e spazio hanno dimensione rispettivamente 0, 1, 2 e 3. Tramite il calcolo vettoriale si definiscono e studiano spazi a dimensione più alta (anche infinita). Gli analoghi “curvi” di questi spazi “piatti” sono le curve e le superfici, di dimensione rispettivamente 1 e 2. Uno spazio curvo in dimensione arbitraria si chiama varietà. Dentro a questo spazio si possono spesso definire punti e rette (dette geodetiche), ma la geometria che ne consegue può non soddisfare gli assiomi di Euclide: una tale geometria è generalmente detta non euclidea. Un esempio è dato dalla superficie terrestre, che contiene triangoli aventi tutti e tre gli angoli retti.
Analisi
L’analisi riguarda principalmente il calcolo infinitesimale, introduce la fondamentale nozione di limite, e quindi di derivata e integrale. Con questi strumenti sono analizzati i comportamenti delle funzioni, che spesso non hanno una descrizione esplicita ma sono soluzioni di una equazione differenziale, derivante ad esempio da un problema fisico.
Settori

Un abaco, un semplice mezzo di calcolo utilizzato fin dai tempi antichi
Come riportato sopra, le discipline principali sviluppate all’interno della matematica sono nate dalla necessità di eseguire calcoli nel commercio, di capire i rapporti fra i numeri, di misurare la terra e di predire eventi astronomici. Questi quattro bisogni possono essere collegati approssimativamente con la suddivisione della matematica nello studio sulla quantità, sulla struttura, sullo spazio e sul cambiamento (cioè, aritmetica, algebra, geometria e analisi matematica). Oltre a queste, vi sono altre suddivisioni come la logica, la teoria degli insiemi, la matematica empirica di varie scienze (matematica applicata) e più recentemente allo studio rigoroso dell’incertezza.
Leggi la definizione direttamente su Wikipedia





