Dal punto di vista esoterico, la Coscienza (Luce) è il Rapporto tra Spirito (Energia) e Sostanza (Materia), E = mc² nella formula di Einstein.
Analogicamente, si può affermare che l’Evoluzione della Coscienza tende alla simmetria sempre più perfetta tra Spirito e Sostanza, alla Loro proporzione aurea: alla Bellezza dell’Essere.
Tra filosofia e scienza, ecco alcuni estratti dal seguente bel discorso sul concetto di simmetria tra Uno e Molti, tra Unitarietà e Differenziazione (la numerazione delle note, i link e le immagini sono a cura della redazione TPS):
Simmetria e rottura di simmetria per comprendere il cambiamento. La tradizione del Timeo in Galileo e Keplero (di A. Briguglia)
“Simmetria e conoscenza.
… In Platone la lontananza dall’Uno per effetto della Diade rimane nascosta nelle cose percepite, come lontananza dal “modello” di cui le cose sono immagini. La simmetria imperfetta, ma pur sempre simmetria, è ciò che rimane nelle cose come ricordo dell’Uno. Cosa può unire due diversi? È la sun-metria, cioé la con-misurabilità.
Nel Timeo compare il termine “sun-metria“; ma esso non è l’equivalente dell’italiano “simmetria”; piuttosto lo è il termine “analoghía“, che conviene tradurre con “simmetria”. Ma analoghía significa proporzione. Nella proporzione, che sia aritmetica, geometria o armonica, un medio proporzionale unisce due grandezze. Essa individua ciò che rimane invariato quando si passa da due grandezze in rapporto tra loro ad altre due.
In Timeo, 31 C Platone scrive che il più bello dei legami è quello che fa di più cose una cosa sola. “E questo per sua natura nel modo più bello compie la analoghía“.
C’è di mezzo la bellezza, intesa come convenienza delle parti, somiglianza, uguaglianza di relazioni, accordo con un principio razionale! Tra proporzione, simmetria, bellezza c’è un circolo ermeneutico, dominato dal ruolo unificante della analoghía.
Il testo citato nella sua interezza dice: “Ma che due cose si compongano bene da sole, prescindendo da una terza, in maniera bella, non è possibile. Infatti, deve esserci in mezzo un legame che congiunga l’una con l’altra. E il più bello dei legami è quello che di se stesso e delle cose legate fa una cosa sola in grado supremo. E questo per sua natura nel modo più bello compie la proporzione (analoghía). Infatti, allorché di tre numeri, o masse o potenze quali si vogliano, il medio sta all’ultimo come il primo sta al medio, e ulteriormente, a sua volta, quello medio sta al primo come l’ultimo sta a quello medio, allora il medio diventando primo e ultimo, e l’ultimo e il primo diventando ambedue medi, in questa maniera di necessità accadrà che tutte le proporzioni siano le stesse, e, divenute fra di loro le stesse, tutte saranno un’unità”. (Timeo 31 C, 32 A, trad. a cura di G. Reale)
In ogni ricerca di simmetria, per gli antichi e per i moderni, è implicita una stessa preoccupazione: trovare ciò che fa di un insieme di elementi le parti di un tutto, tra di loro collegate da relazioni matematiche.
[…] Una simmetria assoluta sarebbe il dominio dell’identico, del non percepibile. Tutto quello che percepiamo è possibile percepirlo perché una simmetria assoluta è stata rotta, altrimenti non esisterebbe niente di definito, di diverso. La simmetria iniziale rimane nascosta nel molteplice dei diversi modi in cui la simmetria può essere rotta.
[…] Perché la scoperta di una simmetria provoca piacere?[1] Platone, ripreso da Keplero, ci dice che questo dipende da un processo di riconoscimento e rimemorizzazione del mondo delle idee che è favorito dal ruolo dianoetico della geometria.
L’idea di Platone è stata ripresa da Jung e Pauli con la teoria degli archetipi. Nel suo commento all’opera di Keplero, Pauli scrive: “Il processo di comprensione della natura, come pure l’intensa felicità che l’essere umano prova nel capire, ossia nel prendere coscienza di una nuova verità, sembra basarsi su una corrispondenza, sulla concordanza tra le immagini interne preesistenti [archetipi] nella psiche umana e gli oggetti del mondo esterno con le loro proprietà. Questa teoria della conoscenza risale notoriamente a Platone ed è sostenuta con grande chiarezza dallo stesso Keplero”. [2]
La tradizione ellenica e la ricerca del principio
Nella storia del pensiero occidentale sulla “natura delle cose” si sono affrontate due tradizioni: quella atomistica, risalente a Leucippo e Democrito, e quella che vede l’identico che permane nelle trasformazioni, non in particelle materiali, ma nella struttura formale. Questa tradizione, originaria della scuola di Pitagora, attraverso il Timeo di Platone, è giunta fino a Galileo e Keplero nel Seicento.
Oggi la teoria dei gruppi di simmetria sembra mettere assieme queste due tradizioni, dal momento che la struttura algebrica di gruppo di trasformazioni gioca il ruolo formale di unificatore delle particelle fondamentali e delle loro interazioni.
A proposito della scuola pitagorica [Aristotele] afferma: “Essi per primi si applicarono alle matematiche e le fecero progredire, e, nutriti delle medesime, credettero che i principi di queste fossero principi di tutti gli esseri. E […] pensarono che gli elementi dei numeri fossero elementi di tutte le cose, e che tutto quanto il ciclo fosse armonia e numero. E tutte le concordanze che riuscivano a mostrare fra i numeri e gli accordi musicali e i fenomeni e le parti del ciclo e l’intero ordinamento dell’universo, essi le raccoglievano e le sistemavano”.
[…] Dalla intuizione pitagorica in poi si pone il problema della natura del numero, della relazione tra forme geometriche, numero e cosmo, della “mente di Dio”.
Creazione di Adamo (da un affresco di Michelangelo)
Si sa che la scuola pitagorica considerò con la massima attenzione i problemi legati alle scale musicali. Ferguson ha seguito la storia della relazione tra musica, fisica e astronomia dal VI secolo a.C. fino alla fisica del Novecento. La corrispondenza tra rapporti numerici e accordi musicali, a partire dall’accordo di quinta, che giocherà un ruolo fondamentale del sistema del mondo di Keplero, ispirò loro l’idea che dietro le cose si nascondessero regolarità esprimibili mediante rapporti tra numeri interi [razionali: frazioni – ndr]: “Nell’universo c’era ordine, e quest’ordine era fatto di numeri. […] Pitagora e i suoi seguaci avevano scoperto anche che c’era evidentemente un potente legame fra le percezioni dei sensi umani e i numeri che pervadevano e governavano ogni cosa. La natura seguiva una logica fondamentale, razionale, bella, e gli esseri umani erano in accordo con essa, non solo a un livello intellettuale (potevano scoprirla e comprenderla) ma anche a quello dei sensi (potevano percepirla attraverso l’udito nella musica)”.
[…] non si è ancora abbastanza riflettuto su quanto le teorie musicali e il concetto di armonia abbiano influito sulla nascita della scienza moderna nel Seicento: “Molti storici della scienza, tra i quali Drake, hanno sottolineato la lacuna che nasce dal trascurare la musica come componente fondamentale che legava tra loro lavori di astronomia, acustica, ottica e fisiologia. Infatti, in quegli anni, scienziati quali Keplero, Mersenne, Galileo, Cartesio, Huygens, Newton, e ancora Eulero, erano profondamente coinvolti nelle discussioni legate ai problemi che venivano classificati come musicali, ma che andavano poi a intrecciarsi con quelle ricerche che a noi oggi sembrano più direttamente collegate allo sviluppo della scienza moderna. […] La teoria musicale diventava in tal modo il punto di incontro tra il mondo astratto del numero e la realtà fisica”. [Vedi Il Suono creatore – ndr.]
La storia comincia con la scuola di Pitagora e con il problema di individuare un termine medio tra due termini: aritmetico, geometrico, armonico.
Le diverse proporzioni venivano poi ascoltate attraverso il monocordo. Si trattava di dividere una corda in due parti con un cavalletto e decidere a quali rapporti tra le parti corrispondesse un suono gradevole.
[…] Platone stesso, nella Repubblica (Politeía) 336 D, rilevò la necessità della matematica come allenamento per la mente che va alla ricerca delle forme; si dice che sulla porta della sua Accademia egli abbia fatto incidere: “Non entri nelle mie porte nessuno che sia ignaro di geometria”. Riguardo alla geometria Platone scrive: “la geometria è effettivamente la conoscenza di ciò che eternamente è”.
Quando Platone tornò ad Atene, dopo la visita al pitagorico Archita a Taranto nel 389 a.C., adottò per la sua Accademia un piano di studi pitagorico: aritmetica, geometria, astronomia, musica.
Nel libro VII della Repubblica, dove si trova la famosa immagine della caverna, l’ascesa dianoetica dalla doxa (opinione) verso la episteme (conoscenza) e dalla eicasia (immaginazione) verso la noesis (intellezione) e la successiva discesa verso il governo dello stato sono descritte come un addestramento che richiede la scienza del numero (524 D, 526 C), la geometria piana (526 C, 527 C), l’astronomia (527 D, 529 C), la scienza dell’armonia (529 C, 531 C). La musica di cui si tratta non è la pratica di “stropicciare le corde”, ma scienza dei rapporti numerici. La scienza degli armonici è indissolubilmente legata nel quadrivio alle altre tre discipline. Ma, nella prospettiva di Platone, devono essere tutte coltivate “in astratto”. Ad esempio l’astronomia deve essere studiata per problemi e non “guardando in su” (529 C).
[…] Nel Timeo Platone espone la sua cosmologia e consegna alla tradizione successiva l’idea che tutto sia retto dalla simmetria, da rapporti e proporzioni. … Si tratta dell’origine dell’universo (cielo, pianeti, uomo, animali) e della sua costituzione. La materia, realtà oscura e indeterminata, “il ricettacolo di tutto ciò che si genera come una nutrice” (49A e 51A), attende di essere informata da un principio. Il Demiurgo convince la necessità cieca, opposta all’intelligenza, e che opera come una causa errante (πλανομενη αιτια, 48A) a condurre verso l’ottimo le cose generate. E l’ottimo è l’impronta dell’uno nel molteplice, operato dalla matematica, forma intermedia tra l’Uno e il molteplice. [3]
All’inizio regnava il caos, “come accade quando il Dio è assente; queste cose che si trovavano in questo stato Egli allora le modellò (διεσκηματισατο) con forme e numeri (ειδεσι τε κατ αριτμοισ)” (53,B)”. Aria, acqua, terra e fuoco, sono realtà mutevoli e non possono essere principi. Principi sono il triangolo rettangolo scaleno, metà dell’equilatero, dal quale si possono comporre il tetraedro (fuoco), l’ottaedro (aria) e l’icosaedro (acqua) e il triangolo rettangolo isoscele dal quale è possibile formare il quadrato e il cubo (terra). Il dodecaedro non può essere formato di triangoli e rappresenta il cosmo. La terra non può così tramutarsi in aria acqua e fuoco, perché fatta di atomi geometrici diversi. Gli elementi sono tenuti assieme dalla proporzione. Le cose concrete non sono aria, acqua, fuoco, terra ma una mescolanza di esse. Cosicché non si può dire “questo è fuoco”, ma “tale è il fuoco”. Questo, possiamo dire, è il “modello standard” secondo Platone!
Euclide dopo Platone formalizzerà la teoria delle proporzioni nel libro V dei suoi Elementi …
Nel Timeo tutte le parti diverse sono tenute insieme attraverso proporzioni. L’anima del mondo, composta della sintesi dell’Identico e del Diverso, è strutturata in parti, secondo i numeri 1, 2, 3, 4, 8, 9, 27. Tale strutturazione rende possibile riconoscere proporzioni nel mondo esterno. Un’ulteriore sottostrutturazione collega le parti mediante proporzioni che riproducono gli accordi della scala pitagorica, il più piccolo dei quali corrisponde a divisioni successive fino a giunger a 256/243, cioè il semitono della scala. La scala cui fa riferimento Platone è quella diatonica introdotta dal pitagorico Filolao.
Keplero: la via delle proporzioni e l’unità del cosmo
Quando si parla del ruolo della simmetria nell’astronomia di Keplero si pensa subito ai cinque poliedri regolari. In realtà il ruolo dei solidi platonici è in Keplero via via sempre più marginale, allusivo e simbolico, limitato alla determinazione del numero dei pianeti, mentre altre simmetrie, basate sugli accordi armonici, acquisteranno sempre più il ruolo di struttura portante del cosmo. 
La sua utilizzazione di simmetrie, con tutte le dovute cautele e distinzioni, presenta sorprendenti analogie con l’uso che se ne fa nella fisica delle particelle. Alla fine della sua fatica Keplero penserà di avere trovato attraverso una struttura formale il modo di tenere insieme numero dei pianeti, distanze dei pianeti dal sole e loro variazioni, periodi di rivoluzione, densità e masse dei pianeti, dimensioni del cosmo […] e poi teologia, anima e forma di governo.
[…] La tradizione dei cinque solidi platonici aveva trovato un’attenta trattazione nel XIII libro degli Elementi di Euclide, cui Keplero si ispirerà. Nel 1509 Luca Pacioli (De Divina Proporzione) testimonierà l’interesse del Rinascimento per i solidi platonici. Leonardo illustrerà l’opera di Pacioli disegnandoli trasparenti e mettendone così in evidenza la struttura. L’innovazione leonardesca sarà ripresa da Keplero nel Mysterium.
Nella Dissertatio cum nuncio sidereo, pubblicata nel 1610, subito dopo avere letto il Nuncius di Galileo, Keplero espone i motivi della sua attenzione per la geometria e per i poliedri regolari: “La geometria è una ed eterna, splendente nella mente di Dio, e la partecipazione ad essa tributata agli uomini è fra le cause per cui l’uomo è immagine di Dio. Ebbene, nella geometria, dopo la sfera, vi è una famiglia di figure che è la più perfetta di tutte, quella dei cinque solidi euclidei. Questo nostro mondo planetario è disposto appunto secondo la regola e il modello di questi solidi”.
[…] Gli unici che accolsero con favore l’opera di Keplero furono Galilei, allora sconosciuto matematico di Padova, e T.Brahe.
[…] L’originalità della astronomia di Keplero, ciò per cui lo possiamo considerare il primo astrofisico, consiste in alcune domande che altri astronomi non si ponevano, considerandole insensate o senza risposta: perché vi sono esattamente un dato numero di pianeti? perché si trovano ad una certa distanza e con una certa velocità? da cosa sono mossi?
Scrive A.Koyré: “Keplero cerca risposte dove nessuno altro vede problemi”. Per Copernico sono ancora le sfere celesti a portare in giro i pianeti, per Bruno sono le animae, Brahe si rifugia in un atteggiamento puramente calcolatorio. Secondo Koyré la domanda, di sapore schiettamente fisico, ha una radice teologica. Keplero considera come unità il sole, le stelle fisse e, cosa decisiva, lo spazio intermedio. Il Sole costituisce la causa motrice, lo spazio il campo nel quale queste forze si propagano. L’idea teologica è considerare i tre come icona della Trinità: il Sole icona del Padre, le Stelle icona del Figlio, lo Spazio intermedio, luogo della creazione, icona dello Spirito.
[…] Nello spazio i solidi del Timeo forniscono la strada per determinare, in modo non arbitrario, il numero dei pianeti. Così tale numero si ottiene come risultato del fatto che il cosmo è creato seguendo certe simmetrie.
[…] Non è comprensibile l’esultanza di Keplero per avere trovato proprio nel rapporto di quinta armonica (3:2) la legge che lega distanze e tempi di rivoluzione, se non si segue quella lunga tradizione di ricercatori (Pitagorici, Tolomeo, Boezio, Giovanni Scoto Eriugena, Copernico etc..) che avevano continuato per lunghi secoli a scrutare il moto dei pianeti (distanze e velocità) per trovarvi rapporti armonici. 
I rapporti armonici erano gli invarianti che legavano il cosmo nel passaggio da un pianeta ad un altro. La ricerca di rapporti armonici era dettata dall’idea che vi dovesse essere una relazione profonda tra l’accordo armonico percepito (anima) e i rapporti numerici relativi ai pianeti (cosmo), tra la musica humana e la musica mundana.
Le orbite ellittiche rompono, per Galileo, la simmetria del cosmo. Per Keplero sono la strada verso la scoperta di simmetrie più profonde consistenti in rapporti e proporzioni tutte generate dal rapporto di quinta armonica. … [Ma anche] quando Keplero rinuncia alle orbite circolari l’archetipo del cerchio e della sfera rimangono fondamentali. Dopotutto il cosmo di Keplero rimane sferico. Dio, anima e cosmo, sono comprensibili attraverso un unico archetipo. Quando i raggi dei pianeti giungendo da angoli opportuni vengono percepiti risuonano come consonanti nell’anima. 
Gli angoli opportuni sono quelli relativi ai poligoni regolari inscritti nel cerchio; la collocazione dei pianeti in modo da essere osservati sotto tali angoli costituisce un “aspetto”. Dai rapporti che si possono combinare con i lati (ad esempio il rapporto di quinta, 3/2, col pentagono [o col Triangolo e il 3° Raggio? – ndr]) scaturiscono gli accordi consonanti della scala pitagorica.
[…] Il progetto platonico di riduzione dei molti all’uno non lo porta verso l’atomismo. Dal Mysterium all’Harmonices il filo conduttore verso l’unità, che lo porterà alla scoperta delle tre leggi e a compiere “la disfatta del circolarismo”, è la ricerca della spiegazione fisica del mondo, della sua struttura armonica.
Anche quando Keplero cercò, nella Strena seu de nive sexangula (1611), la causa della simmetria sexangula della neve non si diresse verso la struttura atomica ma verso motivi formali di efficienza superficie-volume. 
Sono motivi formali che fanno sì che l’uomo e il mondo risuonino allo stesso modo [sostituiremmo motivi formali con funzionali, nel senso che la forma è determinata dalla sua funzione nell’insieme, la quale a sua volta dipende dal principio/archetipo sottostante – ndr]. La proporzione nelle distanze e nelle velocità dei pianeti è tale da essere riconosciuta dalla mente umana che porta in sé come archetipi tali proporzioni.
Le orbite ellittiche sono il risultato della necessità fisica e delle leggi dell’armonia.
Volendo costruire il mondo secondo le leggi dell’armonia non bastano i solidi regolari, che darebbero orbite circolari concentriche e velocità costanti; le proporzioni armoniche costringono il Creatore a far variare le velocità dei pianeti. … In sintesi: dati astronomici (1) + armonia (2) + necessità fisica (3) = orbite ellittiche. I solidi platonici, dopo le osservazioni di Brahe, hanno solo il compito di fissare il numero dei pianeti [fino a Saturno – ndr].
[…] Per costruire l’armonia cosmica Keplero parte da Saturno per il quale tra afelio e perielio abbiamo un accordo di terza maggiore. Partendo da un tono sol [4], l’accordo sarà sol-si. Per costruire le melodie degli altri pianeti occorre dividere per due [riduzione di ottava per la lunghezza d’onda, elevazione di ottava per la frequenza – ndr] le velocità angolari fino ad ottenere toni sulla stessa ottava di Saturno. Ad esempio se dividiamo la velocità angolare della Terra all’afelio per due cinque volte otteniamo 1’47” vicino alla velocità di Saturno all’afelio. La melodia della terra comincerà allora anche con un sol cinque ottave sopra quella di Saturno.
[…] L’accordo tra i pianeti deve essere costruito a partire dal monotono sol della Terra e del mi-mib di Venere [una terza]. Orbite ellittiche e velocità variabili rivelano simmetrie più profonde e nascoste che legano astronomia e musica; si tratta di simmetrie dinamiche rispetto a quelle statiche legate alla forma geometrica.
Rimane il fatto che non si conosce ancora la relazione tra tempo di rivoluzione e distanza. Conoscendola si potrebbe, a partire dai tempi, cioè dall’armonia, trovare le distanze. È una relazione che Keplero ha cercata per più di due decenni e che gli è costata 17 anni di tentativi sui dati di Brahe e che finalmente gli apparve alla mente il 15 maggio del 1618: “è cosa certissima ed esattissima che i tempi periodici di due pianeti qualunque sono precisamente in proporzione sesquialtera delle loro distanze medie, ossia dei loro orbi”. Cioé T1²/ T2²=R1³/ R2³.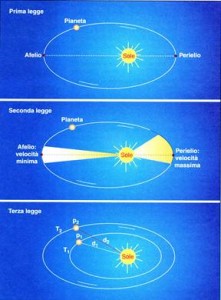
A questo punto Keplero a partire dai tempi di rivoluzione, posta uguale a 1000 la distanza media terra sole, ricava per ogni pianeta semiasse maggiore ed eccentricità e li confronta con i dati di Brahe. “La teoria armonica esce vittoriosa dal confronto con i fatti”.
Il lungo cammino, durato ventiquattro anni, che lo ha portato dalla materialità della forma verso l’armonia, dal Mysterium all’Harmonices, è descritto da Keplero nel libro quinto di quest’ultima opera: “la proporzione che i solidi regolari avrebbero prescritto agli orbi planetari, in quanto inferiore e relativa solo al corpo e alla materia, dovette cedere davanti alle armonie di quel tanto necessario affinché quelle potessero approssimarsi e contribuire alla bellezza dei moti dei globi”.
L’Harmonices è il seguito del Mysterium, l’apogeo di un’ossessione che durò per tutta una vita. Keplero tentava qui, semplicemente, di svelare il segreto fondamentale dell’universo offrendo una vasta sintesi della geometria, della musica, dell’astrologia, dell’astronomia e dell’epistemologia. Era una cosa che nessuno aveva tentato dal tempo di Platone e che nessuno ha più tentato. Dopo Keplero vi è nuovamente la frammentazione dell’esperienza, la scienza si separa dalla religione, la religione dall’arte, la sostanza dalla forma, la materia dallo spirito”.
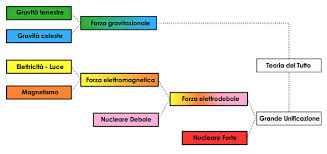
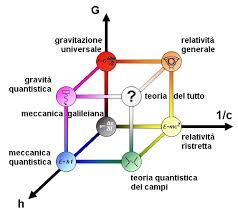
[…] I fisici delle particelle hanno ripreso il sogno di una unificazione, nella quale le teorie abbiano meno costanti ingiustificate. Nella storia della comprensione delle interazioni forti si ha quasi l’impressione che i fisici ad un certo punto si siano preoccupati di costruire teorie semplici ed eleganti seguendo il filo della simmetria e che le abbiano studiate anche quando erano palesemente in contrasto con i dati sperimentali. Animati dalla fiducia che il numero e le masse delle particelle dovessero rispondere ad una logica nella quale la bellezza doveva avere un ruolo. La teoria di Yang e Mills era bella, ma le sue previsioni sembravano in contrasto con il fatto che i bosoni della interazione debole dovevano avere un massa. Occorreva inventare un meccanismo di rottura della simmetria. Un fiume carsico scorreva sotto un approccio puramente fenomenologico in attesa di potere riemergere. Quando è riemerso aveva tutti i connotati del programma di Keplero: spiegare con strutture unificanti il mondo variegato delle interazioni fondamentali.
Dai filosofi ionici fino ad oggi l’idea che la natura sia comprensibile, che sia un libro, che la complicazione del divenire e dei livelli di realtà risponda a vincoli semplici ed eleganti a livello fondamentale non ha mai abbandonato la ricerca.
[…] La storia del modello standard [5] è la conclusione di un lungo percorso, iniziato nel Novecento con Einstein, Heisenberg, Noether, Weyl, Yang e Mills: “Con la comprensione della rottura spontanea di simmetria, i diversi contributi alla fine si sono incontrati nella “standard theory“. È stato questo il ritorno di chi credeva nella bellezza e nella perfezione delle leggi fondamentali della fisica”. È stata forse anche la rivincita di Keplero.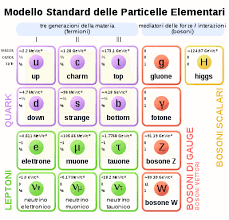
Questo ritorno ha riproposto in modo più pressante un problema che ha alle spalle una lunga tradizione: quello del ruolo della matematica nella comprensione della natura e nella fisica in particolare. La legge di natura formalizzata algebricamente è l’oggetto che tiene insieme fenomeni disparati in un determinato ambito. La simmetria è il vincolo al quale la legge sottostà o deve sottostare se si usa la simmetria come un apriori euristico. La simmetria è definita dal gruppo delle trasformazioni che può subire l’equazione che formalizza la legge, in modo che rimanga covariante.
Ma qual è il significato filosofico di tutto questo? Il problema di Wigner: “quale è la ragione della efficacia della matematica nella fisica” è, come abbiamo visto, molto antico ed è stato girato e rigirato innumerevoli volte.
[…] Se rimaniamo al Seicento possiamo dire che Galileo, Keplero, Cartesio, Boyle, Newton hanno avuto idee diverse sul ruolo della simmetria nelle leggi di natura. Ma tutti si sono posti il problema esplicitamente o implicitamente. Tutti, in modi differenti, condividevano l’idea cristiana [più generalmente, di tutte le tradizioni spirituali – ndr] che un mondo creato dal Logos non poteva che essere intellegibile.
La moderna fisica delle particelle ha acuito il problema dell’efficacia della matematica nella fisica, dal momento che assume il requisito della simmetria come apriori euristico e metodologico […] vincente! Dal 1905 in poi una legge scientifica può essere accettata solo se gode di invarianza rispetto ad un gruppo particolare di trasformazioni. Anzi la legge suprema sembra essere: ogni legge fisica deve essere covariante.
Ma qual è la valenza di realismo delle simmetrie nascoste, visto che non sono accessibili empiricamente, ma lo sono solo i fenomeni conseguenza della rottura della simmetria nascosta? Da dove viene l’asimmetria degli stati se la struttura è simmetrica?
[…] Alle domande già formulate se ne aggiunge un’altra: una sola teoria fisica può tener conto di tutti i fenomeni? Ci sono due aspirazioni marcate nel sentire collettivo: l’aspirazione ad una immagine del mondo unitaria e quella che porta, invece, a marcare le diversità o, addirittura, le differenze. [6]
ll libro della natura è davvero un libro? Boyle, in “Il cristiano virtuoso“, è sicuro: “Il libro della natura è un grande e bell’arazzo arrotolato che non possiamo vedere tutto in una volta, ma dobbiamo accontentarci di attendere la scoperta della sua bellezza e della sua simmetria a poco a poco”. Come Galileo, Keplero, Newton!
[…] Tornando alle considerazioni di Wigner, saremmo allora di fronte a problemi e misteri; questi ultimi sembrano difficilmente gestibili da una qualunque teoria filosofica. Ma siamo di fronte a problemi e misteri che, anziché impoverire o indurre frustrazione, paradossalmente riconducono al senso della vita e della ricerca. […] “Il pieno significato della vita, il significato collettivo di tutti i desideri umani, è fondamentalmente un mistero al di là della nostra comprensione. Da giovane mi irritavo per questo stato di cose. Ma ora mi sono rappacificato con esso. Provo anche un certo onore ad essere associato ad un tale mistero”.
Inizio e fine si specchiano l’uno nell’altro, perciò coincidono.
Il ritmo che li unisce vive nello Spazio,
dove tutto ciò che si duplica si riunisce.
Una Legge presiede in segreto alla libertà senza impedirla:
è la Legge della simmetria proporzionale,
che governa ciò che va dall’Altissimo all’Abissale e li pareggia.
*
Io sono al Centro e sono il Centro in ogni luogo.
Fisso i punti di partenza e di arrivo.
Così produco la Bellezza, che è il segno dell’unione.
(Rituale di Capricornus, 4° aspetto)
(Questo articolo esce in corrispondenza dell’importante allineamento Terra-Venere-Sole, uno dei 5 che disegnano nel Cielo la Stella a 5 punte del Loro Rapporto reciproco ogni 8 anni – vedi Segni del Cielo 2021 – 2° quarto)
[1] Una simmetria perfetta provoca però anche disagio. Occorre sempre che un elemento di rottura, anche nascosto, renda la simmetria più vicina alla vita. È riportato da molti autori e in diverse varianti l’idea che l’introduzione di elementi asimmetrici in arazzi o mosaici sia stata fatta a bella posta per non suscitare l’ira degli dei. Thomas Mann, in un famoso passo della Montagna incantata, fa percepire al protagonista, perdutosi in una tormenta di neve qualcosa di mortale nella “gelida regolarità”, “ostile alla vita” , di ogni fiocco di neve, insieme alla gioia di inventare della natura, dal momento che ogni fiocco era diverso da un altro (Mann, p.418).
[2] Pauli, pp. 60-61. Pauli, al termine del suo lavoro su Keplero, osservava (eravamo nel 1952) che gli scienziati avevano perso l’immagine unitaria del mondo e si chiedeva se era possibile recuperarla. La condizione per il recupero era però che le scienze naturali accettassero di essere solo una parte di tale immagine. [Vedi il testo La Manifestazione – ndr.]
[3] Commenta Dijksterhuis (p.27-28): “L’intero spirito del Timeo è diametralmente opposto a quello dell’immagine del mondo degli Atomisti. Mentre nell’opinione di questi tanto la genesi dell’universo quanto gli eventi che hanno luogo in esso restavano soggetti al cieco caso, nel Timeo un Demiurgo benevolo e saggio trasforma il caos in un cosmo ordinato; mentre gli Atomisti consideravano la vita degli dèi e degli uomini come un caso speciale della universale mobilità degli atomi, Platone fa del mondo un essere vivente fornendo al corpo del mondo un’anima del mondo; mentre gli Atomisti non avevano alcuna risposta da dare ai problemi dell’esistenza dell’universo e del suo scopo, il Timeo spiega l’una e l’altra: la bontà del Demiurgo non poteva permettere il caos, e lo indusse a trasformare la caotica materia spaziale in un tutto armonioso ed equilibrato, che doveva essere quanto più possibile simile a Lui”.
[4] Considerato allora come nota di partenza delle scale musicali e indicato con la lettera gamma γ che indicava anche il punto di incrocio tra eclittica ed equatore celeste, origine del sistema di riferimento per calcolare la posizione degli astri nel cielo.
[5] “Il Modello Standard contempla un certo numero di parametri arbitrari (circa venti), e allo stato attuale delle conoscenze, la teoria sarebbe matematicamente consistente con qualsiasi valore di questi parametri, almeno entro limiti piuttosto ampi. Alcuni di questi parametri determinano, in modo continuo, il modo in cui le simmetrie del Modello Standard sono rotte. Ognuna di queste realizzazioni darebbe vita ad Universi diversi, egualmente consistenti, con una vasta gamma di proprietà fisiche e con diversi modi di evoluzione.” (Maiani in Battimelli, p.57).
[6] Sono, di nuovo, Platone e Aristotele che si fronteggiano. Da una parte l’aspirazione a ricondurre tutto ad una matrice comune: l’Uno. Dall’altra la difesa della autonomia degli esseri, della loro irriducibile diversità, della loro non deducibilità da una base di riduzione. Riduzionismo e antiriduzionismo, attenzione alle parti e al tutto, atomismo e individuazione della sostanza, intesa in senso aristotelico, come ente cui attribuire l’esistenza in senso proprio sono tendenze che ritroviamo, ambedue, tra i fisici, anche se prevale una filosofia riduzionista.”
