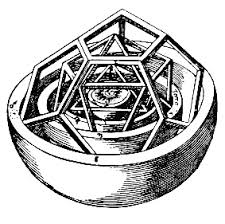
Keplero, nella sua opera “Mysterium cosmographicum”, pubblicata nel 1596, aveva sostenuto l’esistenza di una relazione tra i sei pianeti noti all’epoca (Mercurio, Venere, Terra, Marte, Giove e Saturno) e i solidi platonici.
Come sappiamo, è a Keplero che si deve l’intuizione che le orbite dei pianeti sono ellittiche: tuttavia, al tempo del “Mysterium cosmographicum”, l’astronomo tedesco le considerava ancora circolari, in linea con l’opinione del tempo. Per questo, il sistema solare poteva essere rappresentato come un insieme di cerchi concentrici. Qualche anno prima della sua scoperta Keplero aveva notato che, inscrivendo in un cerchio un triangolo equilatero, e inscrivendo in quest’ultimo un cerchio più piccolo, il rapporto tra il raggio del cerchio maggiore e quello del cerchio minore era uguale al rapporto tra l’orbita di Saturno (cerchio maggiore) e quella di Giove (cerchio minore). Era pertanto possibile tracciare un triangolo equilatero tra le orbite di questi due pianeti. Estendendo il ragionamento, ogni orbita circolare inscriveva (e nel contempo era circoscritta da) uno dei poligoni regolari (triangolo equilatero, quadrato, pentagono regolare, ecc.) in base ad un rapporto predefinito che avrebbe dovuto rappresentare la base geometrica dell’universo.
Non essendo, tuttavia, riuscito a trovare una disposizione dei poligoni regolari che combaciasse univocamente con le sue osservazioni astronomiche, Keplero decise di utilizzare i poliedri regolari (l’estensione dei poligoni regolari in uno spazio a tre dimensioni), stabilendo che ognuno di questi potesse contemporaneamente recare inscritte (ed essere circoscritto da) orbite sferiche.
Se quindi si fossero costruite sei sfere concentriche (le sei orbite dei pianeti noti) e le si fosse posizionate ad intervalli corrispondenti alle dimensioni relative delle orbite dei pianeti (assumendo che questi ruotassero intorno al sole con un’orbita circolare), ciascuna di queste avrebbe potuto inscrivere il solido platonico di ordine minore, ed essere circoscritta dal solido platonico di ordine maggiore.
I solidi erano disposti da Keplero nel seguente ordine (dal più interno al più esterno): ottaedro, icosaedro, dodecaedro, tetraedro, cubo. La concezione geometrica del sistema solare si configurava come segue:
- l’orbita del pianeta più interno (Mercurio) e quella di Venere contenevano un ottaedro;
- l’orbita di Venere e quella della Terra contenevano un icosaedro;
- l’orbita della Terra e quella di Marte contenevano un dodecaedro;
- l’orbita di Marte e quella di Giove contenevano un tetraedro;
- l’orbita di Giove e quella del pianeta più esterno (Saturno) contenevano un cubo.
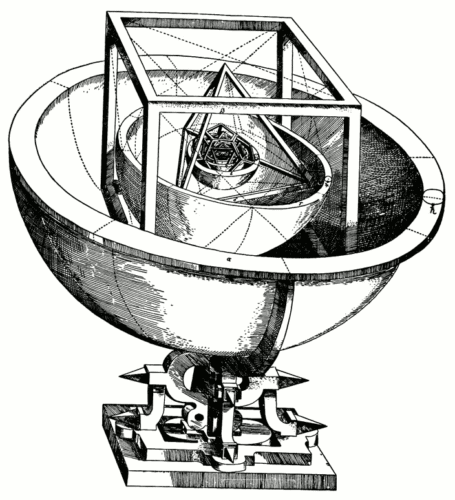
La semisfera esterna rappresenta l’orbita di Saturno; quella contenuta nel cubo rappresenta l’orbita di Giove e quella nel tetraedro l’orbita di Marte, la quale contiene un dodecaedro che al suo interno racchiude la semisfera corrispondente all’orbita della Terra. Dentro di essa vediamo un icosaedro, quindi la semisfera corrispondente all’orbita di Venere, la quale contiene un ottaedro e infine la semisfera che rappresenta l’orbita di Mercurio.
L’idea di Keplero fu abbandonata, in quanto nemmeno l’impiego dei solidi platonici era conciliabile con le osservazioni astronomiche, specie dopo che lo stesso Keplero ebbe scoperto, nel 1609 che “l’orbita descritta da un pianeta è un’ellisse, di cui il sole occupa uno dei due fuochi” (prima legge di Keplero). (Per approfondimenti vedi qui).
Eppure, l’intuizione kepleriana e platonica che alla base di ogni fenomeno naturale e cosmico, e quindi anche dei Cicli solari, vi siano dei Canoni regolatori, armonici o aurei più che aritmetici, risponde alla visione di tutte le tradizioni dell’Antica Saggezza: “Dio geometrizza” e un Ordine di Leggi o volontà coscienti guida l’evoluzione del Tutto verso l’Armonia, la gloria dell’Uno.






