Proporzionalità

Dopo aver praticato alcuni elementi d’Armonica possiamo chiederci se siamo più vicini al Mistero del suono, sulla cui direzione ci ponemmo aprendo il nuovo anno, anzi, più opportunamente, possiamo verificare l’accuratezza del nostro allineamento con esso, perché nel regno delle direzioni i gradi di separazione, siano essi millimetri o anni luce, contano ben poco. Ricapitoliamo alcune generalità, quindi svilupperemo una nuova prospettiva d’osservazione che essendo fondata sulla geometria può essere utile in materia di allineamenti.

Il suono, noto alla Fisica ed all’esperienza sensoriale umana, non pare celare misteri; si conoscono le leggi matematiche che vi corrispondono ed è noto il mezzo materiale in cui si sviluppa, che è poi, tipicamente, anche se non esclusivamente, la stessa aria che respiriamo. La vibrazione elettromagnetica, ad esempio, non è così agevole da descrivere, pur essendo soggetta alle medesime leggi matematiche non dispone di un mezzo materiale in cui svilupparsi; questa assenza ha condotto la scienza verso nuove formulazioni della realtà, che oggi costituiscono la soglia oltre a cui la sfera fisica inizia a mostrare alla vista mentale umana il suo aspetto sottile.

Forse il mistero del suono trapela da alcune cronache antiche diventate ormai leggende o miti e da altre, più recenti, riferite ad esperimenti considerati ormai, però, rami secchi della crescita scientifica; questi elementi convergono, tutti, sulla possibilità d’interazione tra suono e campo gravitazionale, alimentando così il sentimento della sinfonia universale il cui spartito, composto dalle presenze celesti e dai loro ritmi ed equilibri spaziali, è invece inteso dalla moderna Astrofisica come la conseguenza del caos esplosivo iniziale.

Sono segni vaghi che non consentono di precisare il “Mistero del Suono”, ma conosciamo ormai, grazie all’Armonica, un suo corollario, il segreto della proporzionalità, che, certo, è sulla direzione del grande Mistero, manifestato, nella sfera fisica, dalla costellazione della Lira che in un precedente ciclo umano, fu in terra portata dalle mani del cantore Orfeo; del resto sappiamo che ogni strumento sonoro, sia esso di portata cosmica, planetaria o umana deve essere proporzionale, nella sua struttura, per poter suonare.

Anche la proporzionalità, così priva di effetti speciali, pare non nascondere segreti, ma il pensiero proporzionale non è usuale per la mentalità umana che scade facilmente nel più consueto dominio delle misure ‘assolute’, sempre esatte e mai abbastanza precise. Ciò riguarda, in senso lato, il modello del mondo che l’umanità va organizzando, ed in cui, ad esempio, i rapporti armonici con gli altri regni di natura, tra individui, tra nazioni e tra culture, sono tralasciati in nome di valori assoluti ed univoci ma transitori, che occultano la trama proporzionale del creato; essa dovrebbe invece mantenersi ben evidente anche nella sfera della forma, proprio grazie all’opera umana, destinata ad applicare misure finite pur mirando all’infinito manifestato dai rapporti proporzionali, la cui potestà è quella di tracciare la sostanziale unità della manifestazione, solo in apparenza variamente frammentata. Se queste argomentazioni appaiono solo teoriche può essere utile considerarle a fronte dei molti problemi odierni della società e del pianeta che abitiamo. Oltre l’illusione di confortevole sicurezza, propria del mondo occidentale o, come si dice, occidentalizzato, c’è una realtà di grandi squilibri con cui occorre, con urgenza, fare i conti.

L’Armonica, con la sua semplice matematica, è la cartina al tornasole della disposizione mentale umana a tralasciare le ragioni delle relazioni proporzionali; studiandola occorre, infatti, “stare all’erta” cioè, letteralmente, procedere per la massima pendenza, evitando di ripiegare lateralmente sui versanti delle misure finite di frequenza e lunghezza d’onda. L’intervallo sonoro è l’idea stessa di rapporto precipitata in forma vibratoria nel mondo fisico; come tale partecipa, senza veli, alla struttura proporzionale dell’universo, e ci permette, inoltre, di percepirla, udendo. Tale è il potere della forma artistica musicale nelle sue migliori espressioni.

Per mettere a fuoco l’idea di proporzionalità calchiamo ora le orme che alcuni matematici del passato hanno impresso nel campo della geometria. Essi furono, infatti, anche Geometri, maestri con squadra e compasso, e ci hanno lasciato questa elegante analisi dei punti notevoli del triangolo che collegheremo alle tesi proporzionali proprie dell’Armonica.

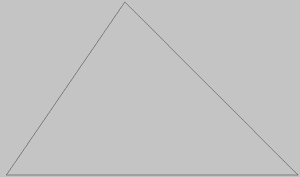
Si ritiene che Euclide fosse discepolo di Platone e che la sua opera monumentale, “Gli Elementi”, avesse lo scopo di fornire una base teorica allo studio dei poliedri regolari: i solidi platonici del Timeo. Egli partì dall’inizio e precisò gli enti geometrici fondamentali nel piano bidimensionale, sviluppando così la geometria piana. Nel piano geometrico si svolge il nostro studio. Disegniamo un triangolo (la prima forma piana) scaleno senza alcun vincolo di misura per gli angoli, quindi anche per lati:

Sappiamo che il triangolo completa la triade geometrica che simboleggia i primi tre intervalli; il punto euclideo, l’ente geometrico fondamentale che sta per l’Unisono, la circonferenza, in altre parole l’amplificazione spaziale del punto, per l’Ottava, ed il triangolo, appunto, il prototipo di tutte le forme complesse che sta per la Quinta, il tessitore del creato.

I triangoli contengono molti punti notevoli; la forma, proprio al livello più elementare, lascia intravedere la formula che attua l’idea creativa ancora astratta. Per il nostro esempio ne consideriamo quattro; i primi tre sono:

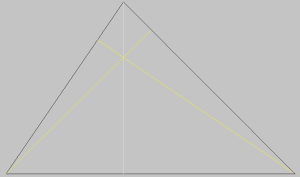
L‘ortocentro che è determinato dalla intersezione delle altezze, cioè dei segmenti che vanno perpendicolarmente da ciascun vertice al lato opposto:

Il circocentro che è determinato dall’intersezione dei segmenti perpendicolari ai lati tracciati dai loro punti medi:

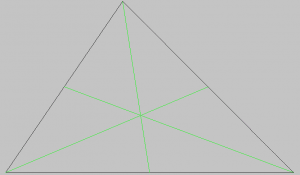
Ed il baricentro che è determinato dall’intersezione dei segmenti che vanno dai vertici ai punti medi dei lati opposti:

Eulero dimostrò che, per tutti i triangoli questi tre punti notevoli giacciono sulla stessa retta (la retta di Eulero), determinando in essa un segmento diviso in due parti di cui l’una è il doppio dell’altra, rispettivamente 2/3 ed 1/3.

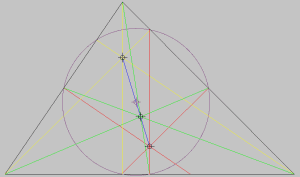
Tireremo tra breve le somme, prima occupiamoci del cerchio di Eulero, o di Feuerbach, detto anche cerchio degli n punti, passante almeno per i tre punti medi di ciascun lato (oltre che per altri punti notevoli che, per brevità, non elenchiamo); il centro di questa circonferenza, l’ultimo punto notevole che consideriamo, giace anch’esso sulla retta di Eulero e la divide in due parti uguali. Siamo autorizzati a stupirci: alcuni matematici eminenti definirono infatti “stupefacenti” queste proprietà. Vediamole in un’unica rappresentazione, al centro del triangolo, in colore blu, è disegnato il segmento su cui giacciono i punti notevoli che abbiamo ricavato.

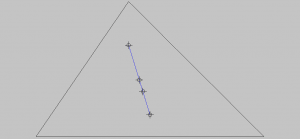
La figura ha ormai assunto una certa complessità; per trarre le nostre conclusioni concentriamo l’attenzione sulla retta di Eulero e sui suoi punti notevoli, togliendo dalla vista tutti gli assi di simmetria e la circonferenza di Feuerbach:

Questo segmento di retta ha una lunghezza e forma un angolo rispetto all’orizzonte costituito dalla base della figura; queste misure dipendono a loro volta dalle dimensioni dei lati e, quindi, da quelle degli angoli ai vertici: ogni triangolo, degli infiniti che possono darsi, ha quindi la sua retta di Eulero, e per ora siamo quindi nel regno delle misure finite.

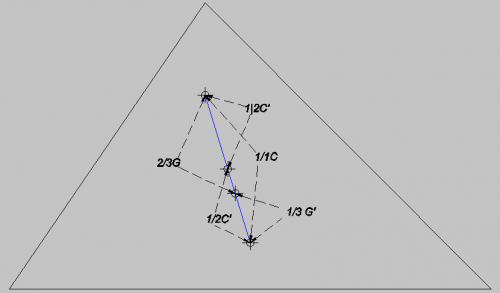
Ora osserviamo la retta dal punto di vista dei rapporti tra i suoi punti notevoli: l’intero segmento, delimitato da ortocentro e circocentro, è suddiviso nelle sue due metà dal centro della circonferenza di Feuerbach, e nei suoi due terzi e, in modo complementare, in un terzo dal baricentro; illustriamo ora questi rapporti, insieme al valore sonoro corrispondente:

Questo è il codice genetico proporzionale della specie geometrica triangolare ed è valido per tutte le sue infinite individualità: solo nel caso del triangolo equilatero la retta si contrae in un punto adimensionale, per ritornare ad espandersi secondo le medesime proporzioni, rotta, anche solo di una parte infinitesima, l’isotropia equilatera.

La retta di Eulero è la corda vibrante di un monocordo geometrico; esprime un certo tono tra le infinite lunghezze d’onda possibili, il suo diapason, e, reiterata nella prima e nella seconda ottava, la sua quinta, com’era nelle premesse alla sezione geometrica di queste note. Essa illustra bene l’evidenza della misura finita, insieme al segreto della proporzionalità, mostrando, per ciascuna modalità, il suo ruolo; la prima (la retta/segmento) è vincolata ed a sua volta vincola alle condizioni contingenti cioè alla forma, la seconda (la proporzionalità) apre alla qualità fondamentale dell’intero campo di manifestazione dei triangoli. Per trovarla abbiamo dovuto faticare un po’ nel piano geometrico perché come tutte le cause è velata dai suoi effetti: le forme materiali. Possiamo ristorarci ascoltando l’accordo di intervalli che vibra in ogni triangolo.

Non risulta che nei testi di geometria vi sia un riferimento diretto alle qualità sonore delle proporzionalità sulla retta di Eulero; è probabile che ci fossero per poi cadere nell’oblio avanzando, nella cultura umana, la disposizione a misurare senza rapportare ed ascoltare. Dopotutto sappiamo che la scuola pitagorica serbava il segreto della proporzionalità sonora, forse troppo prossimo al grande Mistero del Suono.

La spirale delle ottave, che disegnammo a suo tempo, sembra però suggerirci che nel mondo degli uomini tutto deve continuamente mutare, pur senza mai perdersi, anzi innalzandosi di voluta in voluta; il pensiero filosofico, prima ancora che matematico, orfano dell’enfasi proporzionale di Pitagora imboccò il sentiero dell’esattezza formale, confinato nella dimensione contingente, privo di slanci verso la qualità; ma K. Gödel, in anni recenti, dimostrò l’inerente incompletezza di tutti i sistemi coerenti come la matematica, come dire che il ‘reale’ non basta a dimostrare (misurare) se stesso, indicando così una nuova soglia che la mentalità umana dovrà varcare.

In sintonia con ciò non possiamo tacere che, praticando il piano geometrico ed i numeri razionali, quindi i rapporti sonori che come per magia ne scaturiscono, abbiamo evocato il principio stesso dell’irrazionalità; infatti, la circonferenza che così mirabilmente suddivide la retta di Eulero in metà, generando l’intervallo d’ottava, il campo d’esistenza stesso del mondo sonoro, come tutte le forme circolari si regge sul rapporto tra diametro e circonferenza, così facile da realizzare con il compasso, ma alla cui determinazione razionale non sono bastati alcuni millenni d’applicazione dell’ingegno umano, compresi gli ultimi decenni nei quali la potenza di calcolo degli elaboratori elettronici ha solo spostato il problema oltre i 2500 miliardi di cifre decimali non periodiche. Questo numero (π, pi greco), oltre ad essere irrazionale, cioè non esprimibile come frazione di numeri interi, è considerato anche “trascendente” essendo fuori dall’algebra convenzionale. Ad esempio, un altro numero irrazionale celebre, la radice di due, non è trascendente perché può essere pensato come potenziale soluzione dell’equazione algebrica di secondo grado x²=2. Si ritiene che questi due numeri, √2 e π, avessero messo in crisi il sistema pitagorico, in particolare il primo, a cui si giunge, in breve, proprio con il teorema di Pitagora, volendo calcolare l’ipotenusa di un triangolo rettangolo con i due cateti di lunghezza uguale ad uno; ma la formulazione moderna dell’Armonica va oltre l’irrazionalità e la trascendenza. Ponendo all’origine del suo sistema di coordinate tonali 0/0, esso ci fa pensare piuttosto alla categoria filosofica kantiana del “trascendentale” che include ciò che non può esser oggetto di conoscenza pur condizionandola a priori. Questo numero semplicemente non è un numero; infatti si può dimostrare, nella formalizzazione matematica, che per questa frazione sono possibili infinite soluzioni, quindi esprime in sé, potenzialmente, tutti i numeri ed è nessun numero: di esso non si può argomentare. Eppure è la fonte di espansione ed insieme il punto di convergenza di tutti i valori sonori, lungo le rispettive linee equitonali; ciascuna individualità, animata da una scintilla dello stesso fuoco trascendentale, ciascuna sulla sua via, con misure diverse, ma proporzionale con tutte le altre.